數感生活——皮克定理&格子點上的面積
數感生活——皮克定理&格子點上的面積
說到皮克,或許你第一個想到的是《進擊的巨人》裡的皮克小姐,不過今天要來介紹的是奧地利數學家喬治·亞歷山大・皮克(Georg Alexander Pick)。而他所提出的其中一個重要定理「皮克定理」便是今天的主角啦!
▍格子點上的霸主
三角形的面積的求法百百種,無論是大家熟知的「底×高÷2」,或是高中會學到的向量與行列式,面積一直以來都是用「算的」。但是你有沒有想過,面積其實可以用「數的」數出來呢?
⠀⠀
只要頂點在格子點上,三角形面積可以直接套用皮克定理數出來。先數數三角形內部有幾個格子點,記為i;再數三角形的邊上有幾個格子點,記為b。那麼三角形的面積A就會是:
A = i + b/2 – 1
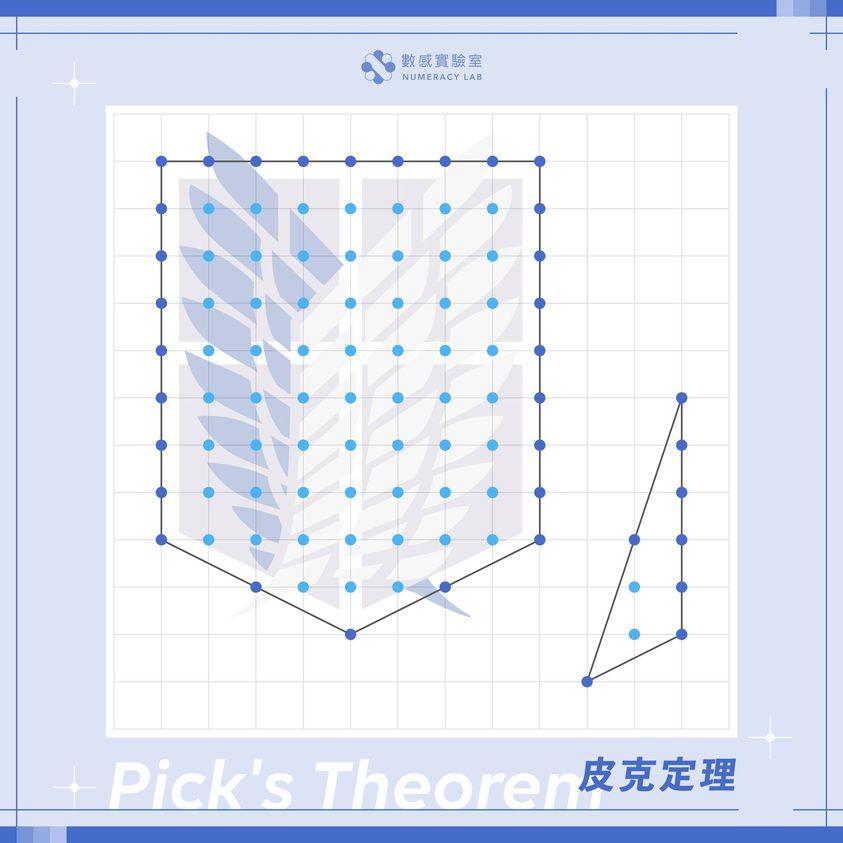
以圖中右下角的三角形為例,i為淺藍色的點,有2個;b為深藍色的點,有8個,套入公式得到:
A = 2 + 8/2 – 1 = 5
和直接計算「底×高÷2」的結果:
A = 5 × 2 ÷ 2 = 5
一樣。
不相信有這麼簡潔的公式的話,再隨手畫幾個三角形便能驗證。而皮克定理其實不限於三角形,只要頂點在格子點上,這條公式可以套用到任何多邊形的面積。不論是凸多邊形、凹多邊形,甚至中間鏤空的圖形,全部都在皮克定理的掌握之中。
⠀⠀
舉例來說,若是將調查兵團徽章如主圖所示放到格子點上,便能照著上述的說明得出面積:
A = 59 + 28/2 – 1 = 72
遇到更複雜的圖形時,皮克定理或許也能夠幫上忙呢!
▍數學老師說重要的是過程
想知道皮克是怎麼突發奇想發現這個性質,或許我們能先降個維度,從數線上的種樹問題著手。如果要求3~7之間的長度,除了直接7減3以外,我們可以換個角度想:每個中間的整數點,都代表著前後0.5的1單位長度(5代表4.5~5.5),而每個邊界點則代表向內的0.5單位長度(7代表6.5~7)。不覺得似曾相識嗎?沒錯,前者就是皮克定理中的i,而後者是b,長度則是i + b/2。
可是,明明皮克定理還有個「-1」,這又是怎麼來的呢?我們不妨從「點周圍的角度」的視角來看。以2×2的正方形來說,有1個內點和8個邊界點,其中邊界點又可區分為邊上的點和頂點。
首先是內點,點周圍的360°都在正方形內,所以代表1單位。
再來是邊上的點,點周圍的180°在正方形內,所以代表1/2單位。
最後是頂點,點周圍的90°在正方形內,所以代表1/4單位。
⠀⠀
最後合計便會是4單位。
⠀⠀
推廣到多邊形內角,我們知道多邊形內角和是
(n-2) × 180° =180°×n – 360°
從剛剛360°代表一個單位,180°是半個單位。所以頂點所代表的單位是
1/2×n-1
後面那個-1,就是推廣到平面後公式為
A = i + b/2 – 1
「-1」存在的原因啦[註1]。
⠀⠀
當然,這畢竟這只是靈感發想的源頭,嚴謹的證明則需要拿出「數學歸納法」,這個部分就請參考留言區的補充資料。
⠀⠀
下次和朋友聊到《進擊的巨人》裡的皮克小姐時,不妨和他們分享另一位數學家皮克所發現的「皮克定理」吧!
⠀⠀
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
[註1] 此說法僅適用於有外角和=360°的凸多邊形。
本文轉貼自數感實驗室,歡迎加入粉絲團。
https://www.facebook.com/numeracylab