布豐投針問題(Buffon’s Needle)─ 經典的圓周率實驗(原理、線上操作)
透過簡單的投針實驗,竟然能夠得到圓周率π的近似值,這就是布豐投針問題(Buffon’s Needle)。
在一張紙上,有平行且等距的線條,現在隨意拋一支針,然後統計針和線條相交的比例。假設線條間距為d,針的長度為L,相交的比例為p。
π = 2L / dp
證明過程需要用到機率論和微積分,有興趣的朋友可以參考影片和文末連結。

操作方法
為了方便運算,只要讓線條間率和針的長度一樣,然後計算1/p=投針數/相交數,再乘以2,就可以得到π的近似值。
例如,投針320次,相交200次,則π的近似值為(320/200)*2=3.2。
也有老師將這個實驗設計成教學活動:Activity: Buffon’s Needle
ps:他建議投火柴,降低實驗受傷風險XD
線上模擬
https://mste.illinois.edu/activity/buffon/#simulation
這網站可以模擬投針實驗,並直接計算π的近似值。
不僅如此,你還可以選擇要投的形狀,共有:直線針、V形針、W形針、3-4-5直角三角形、圓形,甚至還可以自己設計針的形狀!

http://datagenetics.com/blog/may42015/index.html
這網站也可以模擬投針實驗,而且是動態呈現,也就是不直接顯示實驗結果,而是慢慢一針一針丟給你看。可以看到π的值隨著投針次數增加,不斷跳動。
GGB模擬投針
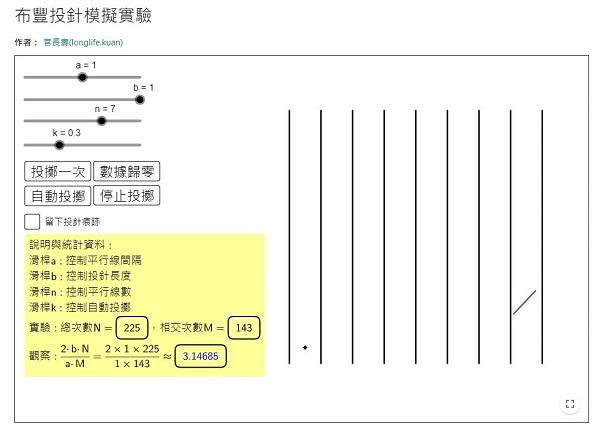
官長壽老師製作的GGB。
https://www.geogebra.org/m/kudz88nt
相關資料
