會考數學會6題就可以拿B?那其他科呢?
前一陣子讀到一篇文章,提到會考的數學,只要會寫6題就可以拿B。
原理如下:
會考數學一共26題,寫對6題,剩下的20題猜對1/4,也就是5題,所以一共可以對11題。
首先,以107年的標準,非選0分的情況下,選擇要對12題才有B,所以應該是要會寫更多題才有B。
我們先不討論詳細策略,以及這策略的利弊。
假設這策略可行,我們統一用「需把握題數」來稱呼「會寫的題數」。
接下來,我們用107年會考為例,算出各科最低「需把握題數」,以及「需把握比例」。
應該可以想像,「需把握比例」也就代表用這個策略拿B的難易度。
要不要先猜一下,哪一科最容易?哪一科最難?
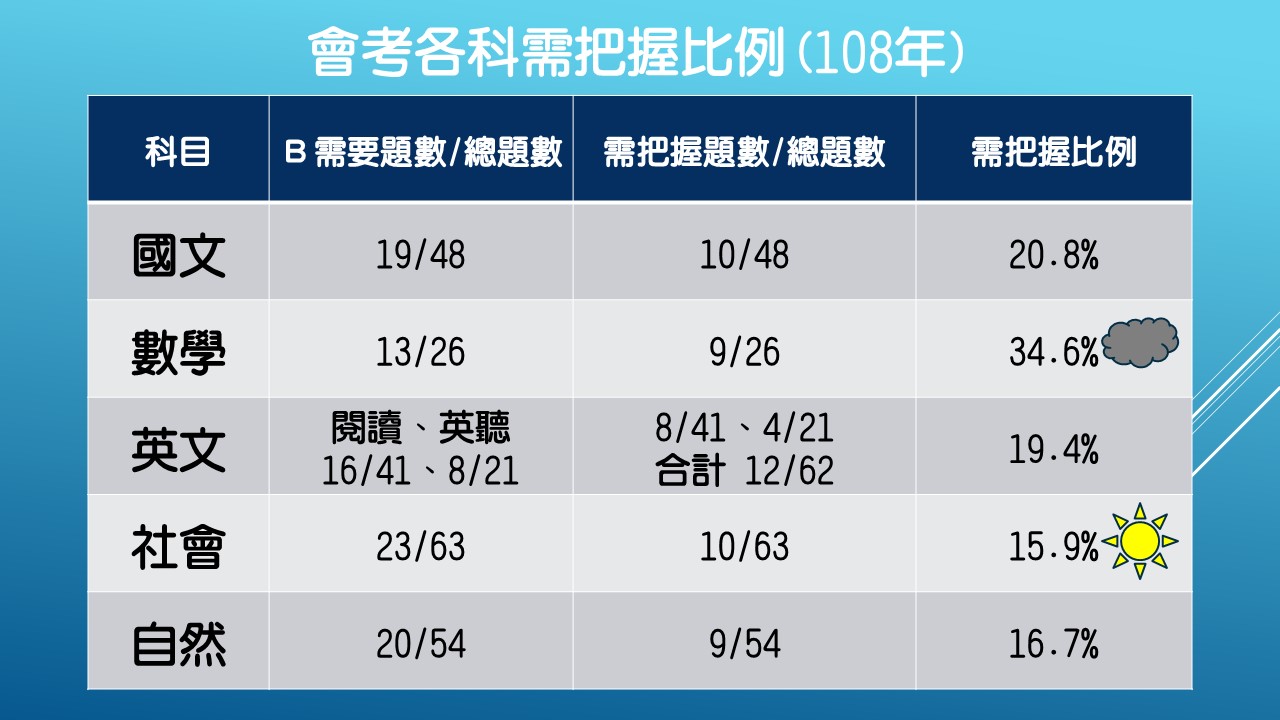
各科需把握比率
恭喜數學科榮獲「最難猜到B」冠軍!
社會科則是拿下「最容易猜B」第一名!
好的,這樣的策略下,數學果然還是最難拿B,畢竟有非選嘛!
所以雖然數學所需題數最少,但因為總題數本來就少,所以難度其實是最高的。
倒是自然和社會的比例都相對低很多,有點意外。
當然,這結果和每年的會考標準有關,所以參考參考就好。
怎麼算出需把握題數?
你會不會好奇這個題數怎麼算出來的?
這其實也是一道數學問題。
以國文為例,總題數48題,得到B需要的題數為19。
假設需把握題數為x。
需把握題數,加上其他題目的1/4,要大於等於B需要的題數。
可以得到下列的不等式:
x + (48-x) × 1/4 ≧ 19
經過幾步的化簡之後,可得到下列的結果。
x ≧ 28 / 3
也就是至少需要把握10題。
有沒有更快的方法?
不想一個數字一個數字試,那就需要解不等式。
不想要一直解不等式,那就用更進階的方法。
假設某一科總題數為N,得到B需要的題數為b,需把握題數為x。
需把握題數,加上其他題目的1/4,要大於等於B需要的題數。
可以得到下列的不等式:
x + (N-x) × 1/4 ≧ b
經過幾步的化簡之後,可得到下列的結果。
x ≧ (4b – N) / 3
這樣就可以很輕鬆的算出需把握的題數了。
數學還是很有用的,對吧!
※會考答題有對有錯,考試前應詳閱各科參考書。
雖然數據是如此,但是扎扎實實的念書,才是得到好成績的最佳策略!
以上分析若有對各科不敬,敬請見諒。
應用在教學中:保妳達B? ─ 不等式的應用