不同投票制度介紹 ─ 波達計數法、兩輪選舉制、排序複選制、孔多塞制 ─ 多數決不一定是最佳方法

我們從小到大都在投票。

選班長，選聚餐地點，選立委，選總統。

幾乎都是多數決，也就是─

少數服從多數，多數尊重少數。

不過，這真的是對團體最好的結果嗎？

 

 

以下要介紹五種投票制度。

先看一下選民分布。

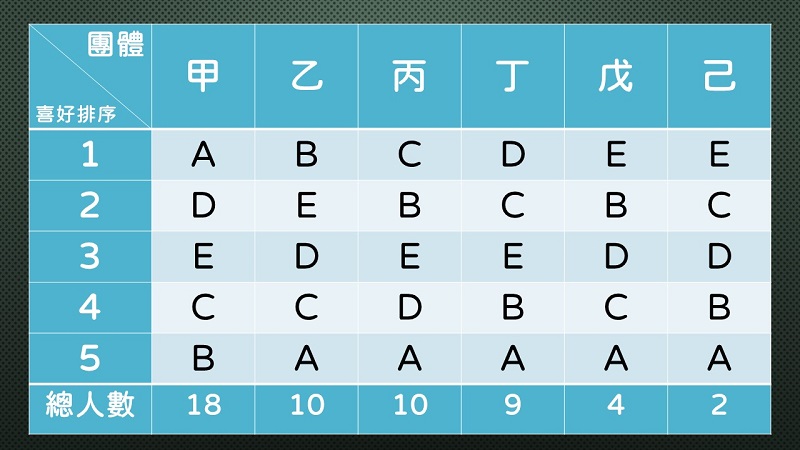
假設選民分成6群，各有不同的支持排序。

例如甲這個團體，最喜歡的選項是A，最不喜歡的選項是B。

（這只是方便說明之後的結果，實際上，大家都知道，30個人可能有30種支持排序。）

 

 

多數決

勝者是：A

最簡單也最暴力的方法。

A選項獲得了最高的18票，所以是贏家。

但是大家看到了嗎？除了甲團外，其他5團一共37人，最不喜歡的都是A！

所以A是靠死忠粉絲集中選票獲勝，但他其實更多黑粉！

假如是選出聚餐地點，那就會出現18人吃到飽，37人吃到吐的狀況。

 

 

波達計數法

勝者是：D。

法國數學家波達（Jean-Charles de Borda）發明的方法。

支持排序第一名得4分，第二名3分，第三名2分，第四名1分，第五名0分。

算出來的結果：

A：72
B：101
C：107
D：136
E：134

上一次的贏家A，成了最後一名。

事實上，MLB和NBA許多投票的獎項，都是這樣選出來的。

 

 

兩輪選舉制

勝者是：B

法國採用的兩輪選舉制，是多數決的改良版。

第一輪得票過半的人，直接當選；

沒有人得票過半，則取最高票的兩名，進行第二輪投票。

因此，A在第一輪只得18票，未過半。

只剩A、B能選的第二輪投票中，甲之外的5個在地團體，集中選票到B，終於扳倒了A政權。XD

 

 

排序複選制

勝者是：C

也可以想成淘汰制，每一輪都剔除最少人支持的選項。

前三輪，E、D、B依序被淘汰，最終決戰中，C大比分擊退了A。

 

 

孔多塞制

勝者是：E

法國政治家及數學家孔多塞侯爵（marquis de Condorcet）發明。

簡單來說，就是兩兩PK，捉對廝殺，也就是單循環賽制。

E不論對上哪一個對手，都能取勝，最終以4勝0敗的成績封王。

 

 

沒有最好的制度，只有最適合的制度

5種制度，5位贏家。

當然是因為，初始的選民分布有特別設計過。

不過也表示，沒有絕對好的制度，只有最適合的制度。

例如全國性的選舉，由於成本考量，就只能使用多數決，或是兩輪選舉制。

班上投票聚餐地點，則可考慮波達計數法或是孔多塞制，避免多數決產生的極端狀況。

多了解幾種方法，就能選出對自己最有利的方法對整個團體而言，最好的方法。