解顆星與相似三角形

打撞球時，有時候會遇到需要「解顆星」的情況，也就是為了閃避某些障礙，所以需要讓母球先撞擊球檯邊緣再擊中目標球。例如底下的例子。

 

假設我們的目標是讓白色的母球利用一顆星，撞擊下方球檯邊後反彈擊中藍色球，那麼該瞄準球檯邊上的哪一個點呢？

 

上圖中的白色就是期望路徑，N點就是我們的目標。

（本段為數學分析，不喜者請自行跳過中間部分，直接看最後一行的結論。）

通過A、C兩點做垂直檯邊的線段，根據「入射角等於反射角」的原理，角ANC必須等於角BND，又角ACN和角BDN都是90度，所以可以根據AA相似性質，得證三角形ANC和三角形BND相似。根據相似三角形對應邊城比例，得到以下結論。

N點必須滿足「CN：DN＝AC：BD」。

常打撞球的大概都知道這個原理，也就是，B點如果越靠近球檯邊，那麼N點的位置就必須越往B點的方向移動。

除了靠經驗累積外，有沒有更準確的方式可以測出N點位置呢？

要利用比例線段幾乎不可能。利用入射角和反射角相等或許可行，但我們對角度的容易有誤差，也不是個容易的方法。

 

上圖可以提供一個穩當的方法。

（本段為數學分析，不喜者請視情況跳過。）

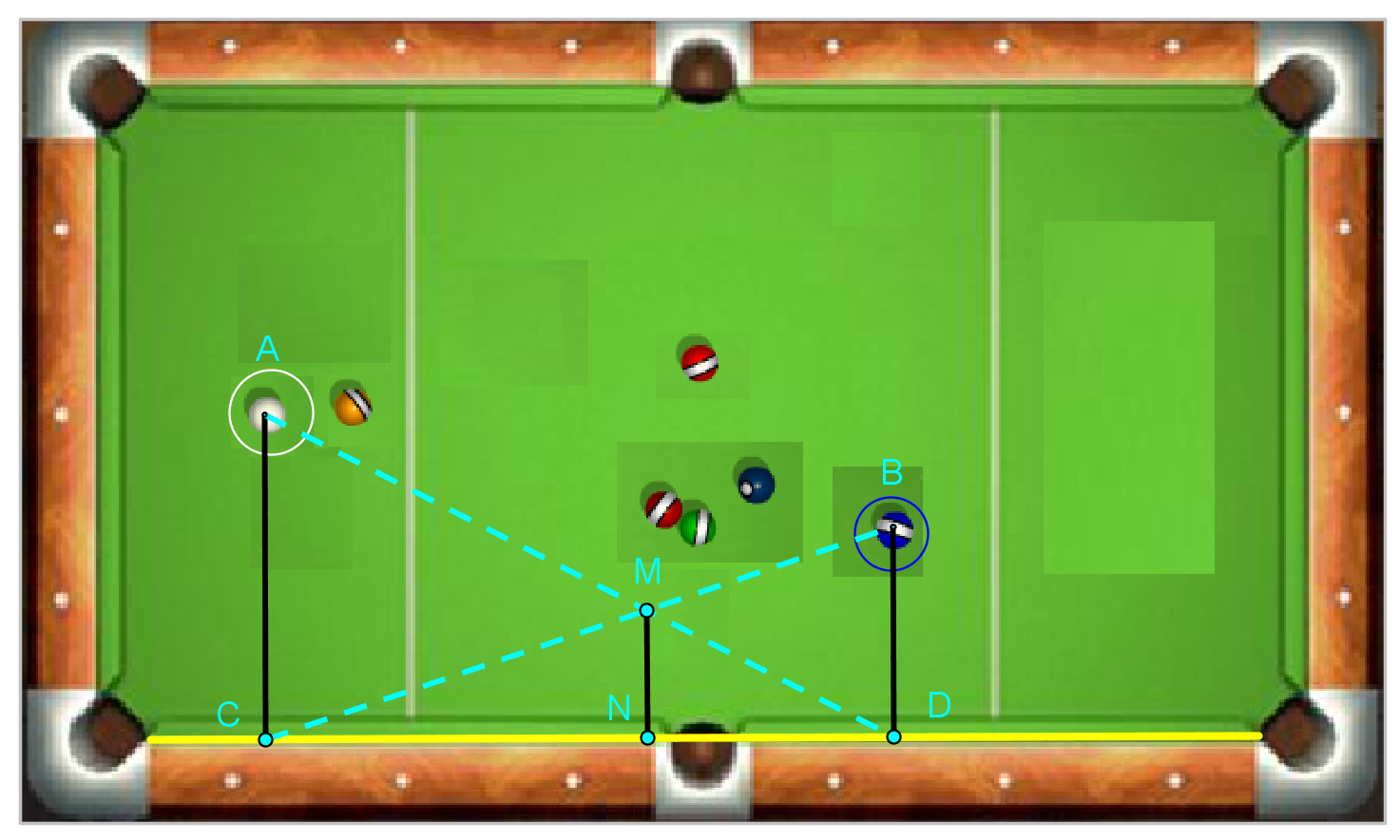
分別連接AD和BC，假設交點為M，過M點做垂直檯邊的線段，所得到的垂足N即為所求。

為什麼呢？有興趣的讀者可以先自行證明看看。

角AMC＝角BMD（對頂角相等），且因為AC平行BD，所以角ACM＝角DBM（內錯角相等）。根據AA相似性質，三角形ACM與三角形DBM相似。因此，AM：DM＝AC：BD。….(1)

在三角形ACD中，因為MN平行AC，根據平行線截等比例線段性質，AM：DM＝CN：DN。….(2)

根據(1)、(2)，得證「CN：DN＝AC：BD」。

也就是，先分別找出母球和目標球垂直檯邊的兩點C、D，然後用球桿比劃出圖中的兩條虛線，通過這兩條虛線的交點做垂直檯邊的垂線，垂足N就是目標。

當然，實際打撞球時要不要用這個方法，就由讀者自行決定了，畢竟需要花點時間，也不夠帥氣。而真正的高手應該是在腦中比劃，或是直接由球感來判斷了。（筆者是屬於比劃老半天後，還是解不到的那類。）

 

熟悉國中數學的老師或學生，對於上面的內容應該不陌生，甚至可以自行證明出來。而最後一張圖的圖形，應該也曾經看過才是，只是題目和所求不同而已。

在相似形的單元裡，如果遇到相關的題目，或許可以用這個撞球問題切入，增添一些趣味。

 

註：本文內容改寫自張海潮教授所著《數學放大鏡》中，「幾何先生G訪問撞球先生B」一文。