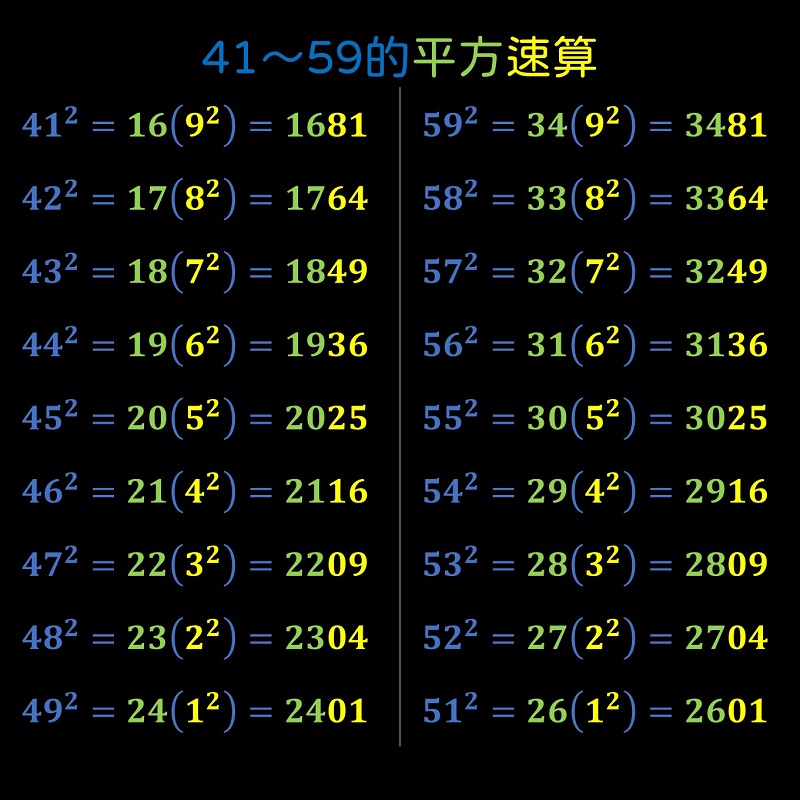
41~59的平方速算 ─ 乘法公式的應用
直接進入主題,請看下方影片或圖片。

蠻漂亮的規律,對吧?
但是,為什麼呢?
(要不要自己先想想看?)
原理說明
我們會用到兩個乘法公式。
首先是49~41的平方,會用到「差的平方」公式。
(a-b)2 = a2-2ab+b2
這裡我們讓a=50。(為什麼?想一想吧!)
(50-b)2 = 502-2×50×b+b2 = 2500-100×b+b2
當b依序代入1~9時,就會得到49~41的平方。
51~59的平方,你應該猜的到,會用到「和的平方」公式。
(a+b)2 = a2+2ab+b2
我們還是讓a=50。(應該知道原因了吧?)
(50+b)2 = 502+2×50×b+b2 = 2500+100×b+ b2
所以,49~41,以及51~59的平方,個位數都是1~9的平方,而百位數則會依序多1。
數學,讓我們能看穿規律背後的原因
首先,不要下「學校怎麼不這樣教」的結論。
說實話,會因為老師教了這個,就比較愛數學,這樣的人有多少?
拿這個例子,當作「數學好有用」的證據,似乎也不太有力。
畢竟,這只是個特例。
我覺得,這個例子可以說明的,是數學「真正的功用」。
當看到這個結論時,我們會覺得很神奇。
而數學,就是可以幫我們解釋「神奇」背後的原理。
不懂數學的,看到表象;
了解數學的,能解釋原因。
當看到一個「神奇」的現象,能夠想到和數學有關,並且試著用數學解釋它。
我想,就是具備數學素養的展現吧。